Os Ângulos Notáveis

Os ângulos , e são chamados notáveis por aparecerem freqüentemente em cálculos. Vamos determinar o seno, cosseno e tangente de cada um deles. Para isso, vamos considerar o triângulo eqüilátero da figura 1:

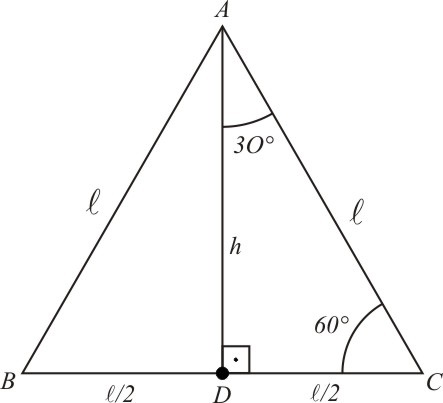
[Figura 1]

Podemos destacar algumas relações:

1) Cada lado do triângulo mede ;

2) é a bissetriz de ;

3) é a mediana de , dividindo em duas partes iguais de tamanho em ;

4) A altura pode ser escrita em função dos lados , da seguinte forma:

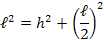
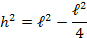
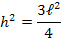
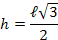
Determinação do seno, cosseno e tangente de e

O seno de um ângulo é definido como a razão do cateto oposto a este ângulo pela hipotenusa do triângulo:

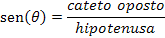
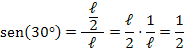
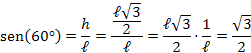
O cosseno de um ângulo é definido pela razão entre o cateto adjacente a este ângulo pela hipotenusa do triângulo:

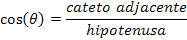
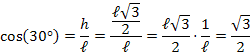
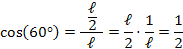
A tangente de um ângulo é definida pela razão entre o cateto oposto pelo cateto adjacente a este ângulo:
 

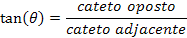
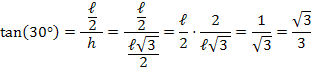
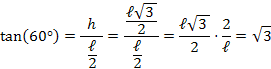
Determinação do seno, cosseno e tangente de

Para calcularmos o seno, cosseno e tangente de , vamos considerar o quadrado mostrado na figura 2:

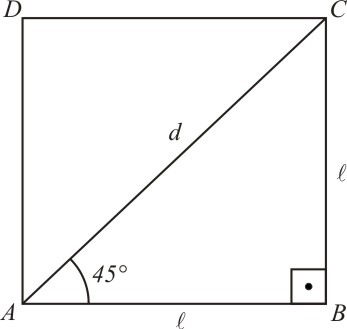
[Figura 2]

A diagonal forma com os lados um ângulo de e podemos escrever a diagonal em função dos lados :

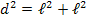
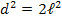
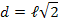
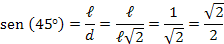
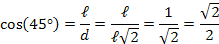
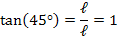
Vamos, agora, construir uma tabela com os ângulos notáveis:

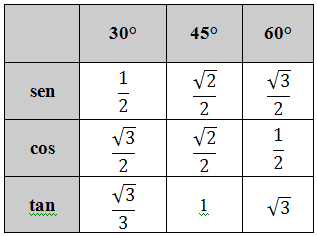
Referências:

[1] http://obaricentrodamente.blogspot.com.br/2010/05/demonstracao-dos-angulos-notaveis.html